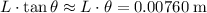Question

Light whose wavelength is 633nm falls on a double slit with spacing of 0.100mm. What is the separation between the 0th and 1st order peak on a screen, L=1.20m from the double slit?

Answer 1

Approximately 0.00760 m (that's 7.60 mm.)

Step-by-step explanation:

Refer to the first diagram attached. For a double-slit diffraction, the angle (angular separation) between the m-th maximum and the central maximum satisfies the following equation:

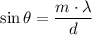`\displaystyle sin(\theta) = (m\cdot \lambda)/(d)`, where

• 
  `\lambda` is the wavelength of the light, and
• 
  `d` is the separation between the two slits.

(Young’s Double Slit Experiment, OpenStaxCollege)

If
`d` is much larger than
`\lambda`, the value of
`\theta` will be considerably small. The value of
`\theta` could thus be approximately as:

`\displaystyle \theta \approx (m\cdot \lambda)/(d)`.

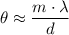For this problem,

• 
  `m = 1` for a first-order maximum.
• 
  `d= \rm 0.100\;mm = 0.100* 10^(-3)\; m`;
• 
  `\lambda = \rm 633\; nm = 633* 10^(-9)\; m`.

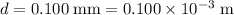Approximate the value of
`\theta`:

`\displaystyle \theta \approx (m\cdot \lambda)/(d) \approx \rm 0.00633\;radians`.

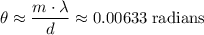Separation between the first and central maximum:

`\displaystyle L \cdot tan(\theta) \approx L\cdot \theta = 0.00760\; \rm m`