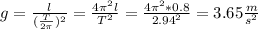Question

Astronauts on the first trip to Mars take along a simple pendulum that has a period on earth of 1.80 s . The period on Mars turns out to be 2.94 s . How long is the pendulum?What is the Martian acceleration due to gravity?

Answer 1

l = 0.8 m

gMars = 3.65 m/s2

Step-by-step explanation:

The period of a pendulum depends on the length of it and the acceleration of gravity according to this equation:

`T = 2 \pi  \sqrt{(l)/(g)}`

If the pendulum has a period of 1.8s on Earth, the length must be:

`l = g * ((T)/(2\pi))^2 = 9.81 * ((1.8)/(2\pi))^2 = 0.8 m`

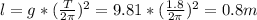
If it has a period of 2.94 s on Mars, the gravity must be:

`g = (l)/(((T)/(2\pi))^2) = (4 \pi^2 l)/(T^2) = (4 \pi^2 * 0.8)/(2.94^2) = 3.65 (m)/(s^2)`