Answer:
Far point of the eye is 22.24 m
Far point of the eye is 0.4 m
Step-by-step explanation:
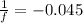
Object distance = u
Image distance = v
Lens equation
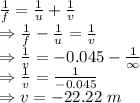
Far point

Far point of the eye is 22.24 m
Object distance = u = 0.25-0.02 = 0.23 m
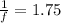
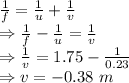
Near point
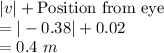
Far point of the eye is 0.4 m