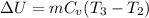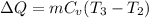Question

A closed system containing an ideal gas undergoes an isentropic expansion process followed by a constant volume heat rejection process. Both processes are reversible. Assuming constant specific heat, write an equation for heat transfer and work for each process.

Answer 1

For isentropic process : Q= 0 ,
`\Delta W=-mC_v(T_2-T_1)`

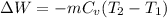
For constant volume :
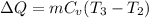`\Delta Q=mC_v(T_3-T_2)`,W=0

Step-by-step explanation:

Given that:

System is closed

In first process ideal gas goes an isentropic expansion and then constant volume heat rejection.

We know that from first law of thermodynamic

Q = ΔU + W

For process 1-2:

Process is adiabatic it means that Q=0

So Q = ΔU + W

0 = ΔU + W

W= -ΔU

We know that internal energy for ideal gas

`\Delta U=mC_v(T_2-T_1)`

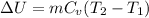
So work W

`\Delta W=-mC_v(T_2-T_1)`

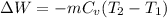
For process 2-3:

Process is constant volume so work transfer will be zero ,W=0

Q = ΔU + W

Q = ΔU + 0

Q = ΔU

`\Delta U=mC_v(T_3-T_2)`

`\Delta Q=mC_v(T_3-T_2)`