Answer:
Option A and D
Explanation:
If a line passes through two points
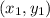 and
and
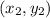 , then the slope of the line is
, then the slope of the line is
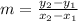
In option A, the function passes through the points (3,-11) and (6,1). So, the slope of the linear function is
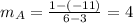
In option B, the function passes through the points (0,3) and (9,5). So, the slope of the linear function is
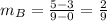
In option C, the function passes through the points (-5,32) and (-1,24). So, the slope of the linear function is
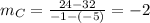
In option D, the function passes through the points (2,0) and (4,8). So, the slope of the linear function is
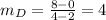
Therefore, the correct option are A and D.