Question

Suppose that we know that of the large fish in a lake the species are 40% perch, 35% bass and 25% trout. (a) What is the probability that a random sample of 5 large fish contains 2 perch, 2 bass, and 1 trout? (b) What is the probability that a random sample of 4 large fish will have more trouts than bass?

Answer 1

a) The probability that a random sample of 5 large fish contains 2 perch, 2 bass, and 1 trout is 14,7%.

b) The probability of the sample having more trouts than bass is 24.46%

Explanation:

a) The probabilities are independent from each other. It means that the probability of selecting a trout, for example, is always going to be 25%, now matter how many trouts have been selected.

A random sample of 5 large fish can contain 2 perch, 2 bass, and 1 trout in many orderings. To simplify our calculus, lets fix the trout at each position. For each position of the trout, there are the following possible combinations of perch and bass.

P - P - B - B

P - B - P - B

P - B - B - P

B - P - P - B

B - P - B - P

B - B - P - P

The trout can be fixed at 5 positions, and for each of this positions there are 6 ways that the basses and perches can be positioned. So there are 5*6 = 30 samples containing 2 perches, 2 basses, and 1 trout.

The probability of 2 perches, 2 basses, and 1 trout being selected is:

`P_(1) = (0.4)^(2)*(0.35)^(2) *(0.25) = 0.049`

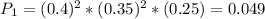
The sample can be permutated in 30 ways: So the probability that a random sample of 5 large fish contains 2 perch, 2 bass, and 1 trout is

P = 30*P1 = 30*0.049 = 0.147 = 14,7%.

b) Sample of 4 fishes.

We can have the following samples with more trouts than bass:

S1: 4 trouts

S2: 3 trouts and one no trout(either perch of bass)

S3: 2 trouts, a bass and a perch

S4: 3 perches and a trout

S5: 2 perches and 2 trouts

The probability that a sample will have more trouts than bass is:

P = P(S1) + P(S2) + P(S3) + P(S4) + P(S5)

P(S1) = (0.25)^4 = 0.0039

For S2, they can be permutated(it can be T-T-NT-T, NT-T-T-T, etc), so

P(S2) = p(4,(3,1))*((0.25)^3)*(0.75) = 4*0.0117 = 0.0468

Where p is permutation of 4 with 3 and 1 repetitions.

For S3, with the permutation

P(S3) = p(4,(2,1,1))*(((0.25)^2)*(0.40)*(0.35)) = 12*0.00875 = 0.105

For S4, there is a permutation

P(S4) = p(4,(3,1))*(((0.40)^3)*0.25)) = 4*0.016 = 0.064

For S5 there is a permutation

P(S5) = p(4, (2,2))*((0.40)^2*(0.25)^2) = 6*0.01 = 0.06

P = 0.0039 +0.0117 + 0.105 + 0.064 + 0.06

P = 0.2446

So, the probability of the sample having more trouts than bass is 24.46%