Answer:
The probability the he or she will answer correctly is 1.5%
Explanation:
In all, there are 18 problems. In this question, the order of which the problems are sorted for the quiz makes no difference. For example, if the question A of the quiz is P1 and question B P2, and question A P2 and question B P1, it is the same thing.
There are 18 problems and 9 are going to be selected. So, there is going to be a combination of 9 elements from a set of 18 elements.
A combination of n elements from a set of m objects has the following formula:
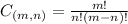
In this question, m = 18, n = 9. So the total number of possibilities is:
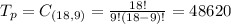
Now we have to calculate the number of desired outcomes. This number is a combination of 9 elements from a set of 13 elements(13 is the number of problems that the student has figured out how to do).
Now, m = 13, n = 9. The number of desired possibilities is:

The probability is the number of desired possibilities divided by the number of total possibilities. So
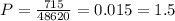
The probability the he or she will answer correctly is 1.5%