Answer:
149.34 Giga meter is the distance d from the center of the sun at which a particle experiences equal attractions from the earth and the sun.
Step-by-step explanation:
Mass of earth = m =

Mass of Sun = M = 333,000 m
Distance between Earth and Sun = r = 149.6 gm = 1.496\times 10^{11} m[/tex]
1 giga meter =
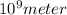
Let the mass of the particle be m' which x distance from Sun.
Distance of the particle from Earth = (r-x)
Force between Sun and particle:
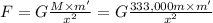
Force between Sun and particle:
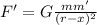
Force on particle is equal:
F = F'

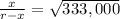 = ±577.06
= ±577.06
Case 1:
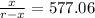
x =
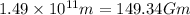
Acceptable as the particle will lie in between the straight line joining Earth and Sun.
Case 2:
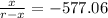
x =
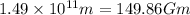
Not acceptable as the particle will lie beyond on line extending straight from the Earth and Sun.