Question

Calculate the distance d from the center of the sun at which a particle experiences equal attractions from the earth and the sun. The particle is restricted to the line which joins the centers of the earth and the sun. Justify the two solutions physically. Note that: mearth = 5.976 x 1024 kg msun = 333,000 mearth Distance earth to sun = 149.6 Gm (giga-meters).

Answer 1

149.34 Giga meter is the distance d from the center of the sun at which a particle experiences equal attractions from the earth and the sun.

Step-by-step explanation:

Mass of earth = m =
`5.976* 10^(24) kg`

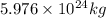
Mass of Sun = M = 333,000 m

Distance between Earth and Sun = r = 149.6 gm = 1.496\times 10^{11} m[/tex]

1 giga meter =
`10^(9) meter`

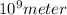
Let the mass of the particle be m' which x distance from Sun.

Distance of the particle from Earth = (r-x)

Force between Sun and particle:

`F=G(M* m')/(x^2)=G(333,000 m* m')/(x^2)`

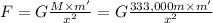
Force between Sun and particle:

`F'=G(mm')/((r-x)^2)`

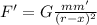
Force on particle is equal:

F = F'

`G(333,000 m* m')/(x^2)=G(mm')/((r-x)^2)`

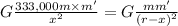
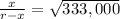`(x)/(r-x)=√(333,000)` = ±577.06

Case 1:

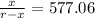
`(x)/(r-x)=577.06`

x =
`1.49* 10^(11) m=149.34 Gm`

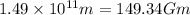
Acceptable as the particle will lie in between the straight line joining Earth and Sun.

Case 2:

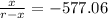
`(x)/(r-x)=-577.06`

x =
`1.49* 10^(11) m=149.86 Gm`

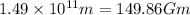
Not acceptable as the particle will lie beyond on line extending straight from the Earth and Sun.