Question

What is the polynomial function of lowest degree with lead coefficient 1 and roots i, -2 and 2?

Answer 1

Explanation:

the polynomial function is; (x - i)(x-2)(x+2)

Answer 2

`P(x)=x^3-ix^2-4x+4i`

Explanation:

We have to find the polynomial of lowest degree with lead coefficient 1 and roots i, -2 and 2.

A polynomial can be written as:

`P(x)=a*(x-x_1)*(x-x_2)*...*(x-x_n)`

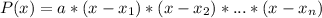
Where
`a` is the lead coefficient. And
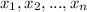`x_1,x_2,...,x_n` are the roots of the polynomial.

Then we have
`a=1` and,

`x_1=i\\x_2=-2\\x_3=2`

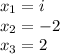
We can write the polynomial as:

`P(x)=1(x-i)(x-(-2))(x-2)\\P(x)=(x-i)(x+2)(x-2)`

You can apply squared binomial to
`(x+2)(x-2)`:

`(x+2)(x-2)=x^2-2^2=(x^2-4)`

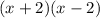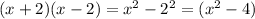
Then,

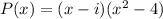`P(x)=(x-i)(x^2-4)` apply distributive property:

`P(x)=(x-i)(x^2-4)\\P(x)=x^3-4x-ix^2+4i\\P(x)=x^3-ix^2-4x+4i`

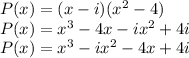
The the polynomial of lowest degree with leaf coefficient 1 and roots i, -2 and 2 is:

`P(x)=x^3-ix^2-4x+4i`