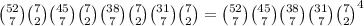Question

b) How many ways can you deal cards (from a deck of 52) to 4 people when each player gets 7 cards. 2 hidden and 5 visible. Assume that order does not matter among hidden and visible cards.

Answer 1

`{52 \choose 7}{45 \choose 7}{38 \choose 7}{31 \choose 7}{7 \choose 2}^4`

Explanation:

The dealing of the cards can be seen in the following way:

We first have to choose which 7 cards are going to be dealt to the 1st player. So we have to pick 7 cards out of the 52 available cards. This can be done in
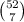`{52 \choose 7}` ways. Now that we have chosen which 7 cards are going to be dealt to the 1st player, we have to choose which 2 of them are going to be the hidden ones. So we have to pick 2 cards out of the 7 cards to be the hidden ones. This can be done in
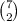`{7 \choose 2}` ways. At this point we now know which cards are being dealt to the 1st player, and which ones are hidden for him. Then we have to choose which 7 cards to deal to the 2nd player, out of the remaining ones. So we have to pick 7 out of 52-7=45. (since 7 have been already dealt to the 1st player). This can be done in
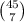`{45 \choose 7}`. Then again, we have to pick which 2 are going to be the hidden cards for this 2nd player. So we have to pick 2 out of the 7. This can be done in
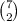`{7 \choose 2}` ways. Then we continue with the 3rd player. We have to choose 7 cards out of the remaining ones, which at this point are 52-7-7=38. This can be done in
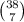`{38 \choose 7}`. And again, we have to choose which ones are the hidden ones, which can be chosen in
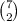`{7 \choose 2}` ways. Finally, for the last player, we choose 7 out of the remaining cards, which are 52-7-7-7=31. This can be done in
`{31 \choose 7}` ways. And choosing which ones are the hidden ones for this player can be done in
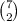`{7 \choose 2}` ways. At the end, we should multiply all our available choices on each step, to get the total choices or total ways to deal the cards to our 4 players (since dealing the cards is a process of several steps with many choices on each step).

`{52 \choose 7}{7 \choose 2}{45 \choose 7}{7 \choose 2}{38 \choose 7}{7 \choose 2}{31 \choose 7}{7 \choose 2}={52 \choose 7}{45 \choose 7}{38 \choose 7}{31 \choose 7}{7 \choose 2}^4`