Question

Air in a piston-cylinder device is compressed from 25 C and 100 kPa to 500 kPa during a polytropic process for which PV.3- constant. The air temperature after compression (in C) is : (a) 182 (b) 156 (c) 1207 (d) 115

Answer 1

T2=871.34 K = 598.19 °C

Step-by-step explanation:

As the relation Pv^k=cte is not clear, I will assume that k=3

Now, the first step is to find the specific molar volume in state 1, we use ideal gas law to find it:

`P_(1) \\u _(1)=RT_(1)\\\\P_(1)=100 kPa\simeq 1atm\\\\\\u _(1)=(RT_(1))/(P_(1)) \\\\\\u _(1)=24.44L/mol`

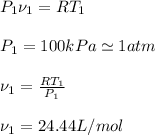
Now, to find the value of v2, we use the polytropic relation:

`P_(1) \\u _(1) ^(3)=P_(2) \\u _(2) ^(3)\\\\\\u _(2) ^(3)=(P_(1) \\u _(1) ^(3))/(P_(2)) \\\\\\u _(2)=\sqrt[3]{(P_(1) \\u _(1) ^(3))/(P_(2))} \\\\\\u_(2)=14.29L/mol`

With the value of v2, we can calculate the temperature in the second state with ideal gas law:

`P_(2) \\u _(2)=RT_(2)\\\\T_(2)=(P_(2) \\u _(2))/(R) \\\\T_(2)=871.34K`