Question

Determine whether the following are spontaneous or non-spontaneous under standard conditions:

Ca(s) + Cd2+(aq) ® Ca2+(aq) + Cd(s)

2 Br-(aq) + Sn2+(aq) ® Sn(s) + Br2(l)

Answer 1

For 1: The above reaction is non-spontaneous.

For 2: The above reaction is non-spontaneous.

Step-by-step explanation:

• For 1:

The given chemical reaction: follows:

`Cd^(2+)(aq.)+Ca(s)\rightarrow Ca^(2+)(aq.)+Cd(s)`

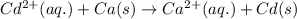
Here, cadmium is getting reduced because it is gaining electrons and calcium is getting oxidized because it is loosing electrons.

We know that:

`E^o_((Cd^(2+)/Cd))=-0.40V\\E^o_((Ca^(2+)/Ca))=-2.87V`

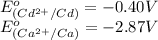
Substance getting oxidized always act as anode and the one getting reduced always act as cathode.

To calculate the
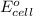`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

`E^o_(cell)=-0.40-(-2.87)=2.47V`

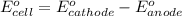
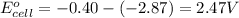
Relationship between standard Gibbs free energy and standard electrode potential follows:

`\Delta G^o=-nFE^o_(cell)`

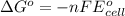
As, the standard electrode potential of the cell is coming out to be positive for the above cell. Thus, the standard Gibbs free energy change of the reaction will become negative making the reaction spontaneous.

Hence, the above reaction is spontaneous.

• For 2:

The given chemical reaction: follows:

`2Br^-(aq.)+Sn^(2+)(aq.)\rightarrow Br_2(l)+Sn(s)`

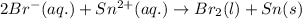
Here, tin is getting reduced because it is gaining electrons and bromine is getting oxidized because it is loosing electrons.

We know that:

`E^o_((Sn^(2+)/Sn))=-0.14V\\E^o_((Br_2/2Br^-))=-1.07V`

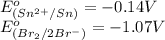
Substance getting oxidized always act as anode and the one getting reduced always act as cathode.

To calculate the
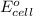`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

`E^o_(cell)=-0.14-(1.07)=-1.21V`

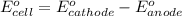
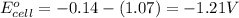
Relationship between standard Gibbs free energy and standard electrode potential follows:

`\Delta G^o=-nfE^o_(cell)`

As, the standard electrode potential of the cell is coming out to be negative for the above cell. Thus, the standard Gibbs free energy change of the reaction will become positive making the reaction non-spontaneous.

Hence, the above reaction is non-spontaneous.