Question

The acceleration of a particle is given by a = −kt2 , where a is in meters per second squared and the time t is in seconds. If the initial velocity of the par- ticle at t = 0 is v0 = 12 m /s and the particle takes 6 seconds to reverse direction, determine the mag- nitude and units of the constant k. What is the net displacement of the particle over the same 6-second interval of motion?

Answer 1

Assuming that
`a=-k * t^(2)` ; k = 1/6 ≅ 0.167

Step-by-step explanation:

Since it takes the particle 6 seconds to reverse direction, we can say that:

`v_(f) = v_(o) -k\int\limits^6_0 {t^(2)} \, dx`

From that equation we get:

`0 = 12-(k*6^(3))/(3)`

And now, if we solve for k, we get:

`k=(1)/(6)`

Answer 2

The constant value is
`k\approx 0.17\,m/s^4`

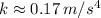
The net displacement is
`D=53.64\, m`

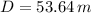
Step-by-step explanation:

If the acceleration as a function of time is given
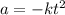`a=-kt^2` then, first of all, knowing that the units of acceleration should be
`m/s^2` we should have
`[k]=m/s^4` where
`[k]` stands for The dimension of k (these are just the units of k in a less formal way of saying it.

On the other hand we have only information about the velocity, but we only have the acceleration function, it turns out we can integrate the expression of acceleration in order to obtain the velocity as a function of time:

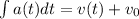`\int a(t) dt=v(t)+v_0` where
`v_0` as a constant of integration which should have units of
`[v_0]=m/s` in order to be consistent with the fact that it is a velocity function, it is therefore natural to think of
`v_0` as the initial velocity of the the particle.

Let's now get our hands dirty by integrating
`a(t)`

`v(t)=\int -kt^2 dt=-k\int t^2 dt=-k(t^3)/(3)+v_0`.

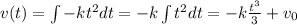By having the velocity as a function of time we can now use the conditions given at t=0 and t=6.

At t=0 we have:

`v(0)=-k(0^3)/(3)+v_0=12\implies v_0=12\, m/s`

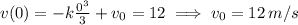
At t=6 the particle start reversing direction, that means at that very instant it velocity should be zero in order to start traveling the other way. This can only mean the following

`v(6)=-k(6^3)/(3)+12=0\implies k=v_0\cdot(3)/(6^3)\approx0.17 \, m/s^4`.

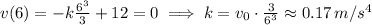We have a full description now of the acceleration and the velocity function. In order to get the net displacement we need to integrate the velocity function

`x(t)=\int v(t)=-(k)/(3)\int 3 dt+\int v_0 dt=-(k)/(12)t^4+v_0\cdot t+x_0`

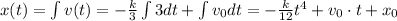
Where
`x_0` is the initial displacement. If we subtract
`x_0` on both sides we get the net displacement or distance traveled

`x(t)-x_0=D=-(kt^4)/(12)+12t`

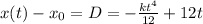
Plugging the value of 6 above gives us the net displacement

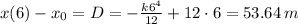`x(6)-x_0=D=-(k6^4)/(12)+12\cdot 6=53.64 \, m`.