Answer:
Option C.
Explanation:
It is given that lines a and b are cut by transversal f.
If a transversal line intersect two parallel lines, then the alternate exterior angles are same.
We need to find the value of x so that lines a and b are parallel lines cut by transversal f.
So, equate both alternate exterior angles.
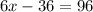
Add 36 on both sides.
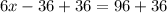
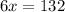
Divide both sides by 6.
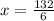
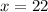
The value of x is 22. Therefore, the correct option is C.