Answer:
The wavelength of the emitted photon will be approximately 655 nm, which corresponds to the visible spectrum.
Step-by-step explanation:
In order to answer this question, we need to recall Bohr's formula for the energy of each of the orbitals in the hydrogen atom:
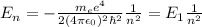 , where:
, where:
[tex]m_{e}[tex] = electron mass
e = electron charge
[tex]\epsilon_{0}[tex] = vacuum permittivity
[tex]\hbar[tex] = Planck's constant over 2pi
n = quantum number
[tex]E_{1}[tex] = hydrogen's ground state = -13.6 eV
Therefore, the energy of the emitted photon is given by the difference of the energy in the 3d orbital minus the energy in the 2nd orbital:
[tex]E_{3} - E_{2} = -13.6 eV(\frac{1}{3^{2}} - \frac{1}{2^{2}})=1.89 eV[tex]
Now, knowing the energy of the photon, we can calculate its wavelength using the equation:
[tex]E = \frac{hc}{\lambda}[tex], where:
E = Photon's energy
h = Planck's constant
c = speed of light in vacuum
[tex]\lambda[tex] = wavelength
Solving for [tex]\lambda[tex] and substituting the required values:
[tex]\lambda = \frac{hc}{E} = \frac{1.239 eV\mu m}{1.89 eV}=0.655\mu m = 655 nm[tex], which correspond to the visible spectrum (The visible spectrum includes wavelengths between 400 nm and 750 nm).