Question

Calculate the wavelength of light emitted when each of the following transitions occur in the hydrogen atom. What type of electromagnetic radiation is emitted in each transition? n=3 --> n=2

Answer 1

The wavelength of the emitted photon will be approximately 655 nm, which corresponds to the visible spectrum.

Step-by-step explanation:

In order to answer this question, we need to recall Bohr's formula for the energy of each of the orbitals in the hydrogen atom:

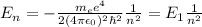`E_(n) = -(m_(e)e^(4))/(2(4\pi\epsilon_(0))^2\hbar^(2))(1)/(n^2) = E_(1)(1)/(n^(2))`, where:

[tex]m_{e}[tex] = electron mass

e = electron charge

[tex]\epsilon_{0}[tex] = vacuum permittivity

[tex]\hbar[tex] = Planck's constant over 2pi

n = quantum number

[tex]E_{1}[tex] = hydrogen's ground state = -13.6 eV

Therefore, the energy of the emitted photon is given by the difference of the energy in the 3d orbital minus the energy in the 2nd orbital:

[tex]E_{3} - E_{2} = -13.6 eV(\frac{1}{3^{2}} - \frac{1}{2^{2}})=1.89 eV[tex]

Now, knowing the energy of the photon, we can calculate its wavelength using the equation:

[tex]E = \frac{hc}{\lambda}[tex], where:

E = Photon's energy

h = Planck's constant

c = speed of light in vacuum

[tex]\lambda[tex] = wavelength

Solving for [tex]\lambda[tex] and substituting the required values:

[tex]\lambda = \frac{hc}{E} = \frac{1.239 eV\mu m}{1.89 eV}=0.655\mu m = 655 nm[tex], which correspond to the visible spectrum (The visible spectrum includes wavelengths between 400 nm and 750 nm).