Question

A certain forest covers an area of

4500 km2. Suppose that each year this area decreases by 8.75%. What will the area be after 6 years?
Use the calculator provided and round your answer to the nearest square kilometer.

Answer 1

2598 square kilometers

Explanation:

Hello

Step 1

year one

using a rule of three is possible to find how much is 8.75 od 4500 km2

Let

if

4500 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`4500:100\\x:8.75\\(4500)/(100)=(x)/(8.75)\\x=(4500*8.75)/(100) \\x=393.75\\`

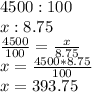
at the end of the year one, the area will be

4500-393.75=4106.25

this will be the initial area for the year 2.

Step 2

repite the step 1 with area initial =4106.25 km2

4106.25 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`4106.25:100\\x:8.75\\(4106.25)/(100)=(x)/(8.75)\\x=(4106.25*8.75)/(100) \\x=359.29\\`

at the end of the year 2, the area will be

4106-359.29=3746.70

this will be the initial area for the year 3.

Step 3

repite the step 1 with area initial =4106.25 km2

3746.70 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`3746.70:100\\x:8.75\\(3746.70)/(100)=(x)/(8.75)\\x=(3746.7*8.75)/(100) \\x=327.83\\`

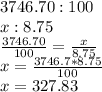
at the end of the year 3, the area will be

3746.70-327.83=3419.09

this will be the initial area for the year 4.

Step 4

year four

repite the step 1 with area initial =3419.09 km2

3419.09 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`3419.09:100\\x:8.75\\(3419.09)/(100)=(x)/(8.75)\\x=(3419.09*8.75)/(100) \\x=299.17\\`

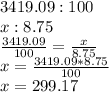
at the end of the year 4, the area will be

3419.09-299.173=3119.82

this will be the initial area for the year 5.

Step 5

year five

repite the step 1 with area initial =3119.82 km2

3119.82 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`3119.82:100\\x:8.75\\(3119.82)/(100)=(x)/(8.75)\\x=(3119.82*8.75)/(100) \\x=272.99\\`

at the end of the year 5, the area will be

3119.82-272.99=2846.92

this will be the initial area for the year 6.

Step 6

year six

repite the step 1 with area initial =2846.92km2

2846.92 km2 ⇒ 100$

x?km2 ⇒8.75

do the relation and isolate x

`2846.92:100\\x:8.75\\(2846.92)/(100)=(x)/(8.75)\\x=(2846.92*8.75)/(100) \\x=249.10\\`

at the end of the year six, the area will be

2846.92-249.10=2597.82 square kilometers

Have a great day.