Question

Redesigned Computers has 8 percent coupon bonds outstanding with a current market price of $889.83. The yield to maturity is 9.34 percent and the face value is $1,000. Interest is paid semiannually. How many years is it until this bond matures?

Answer 1

years to maturity:

Step-by-step explanation:

The market value will be the present value of the bons at 9.34% YTM

Present value of the cuopon payment will be an aordinary annuity:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 40 (1,000 x 8%/2 payment per year

time n (unknow value)

rate 0.0934

`40 * (1-(1+0.0467)^(-n) )/(0.0467) = PV_c\\`

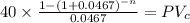
Present value of the maturity, which is present value of a lump sum

`(Maturity)/((1 + rate)^(time) ) = PV`

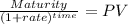
Maturity 1,000.00

time n

rate 0.0467 (rate / 2 as there are 2 payment per year)

`(1000)/((1 + 0.0467)^(n) ) = PV_m`

We know that:

PVc + PVm = Market price = 889.83

So we can build this equation:

`40 * (1-(1+0.0467)^(-n) )/(0.0467) + (1000)/((1 + 0.0467)^(n) )  = 889.83\\`

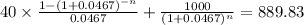
Based on the values we are given, we solve for "n"

First, we work out the annuit y formula:

Then we do common factor:

`1.0467^(-n) * ( 1000 - (40)/(0.0467)) = 889.83 - (40)/(0.0467)  \\`

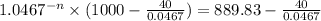
We solve and leave this:

`1.0467^(-n)  * 143,689507 = 33.29895075`

`1.0467^(-n)  = 0.232098657`

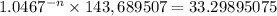
We now apply logarthimic properties to sovle for n

`-n  = (log 0.232098657)/(log  1.0467)`

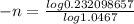
n = 32 These are semiannual payment, so we divide by 2 to convert to year:

32/2 = 16 years