Question

John says that the value of the function cos[ω(t + T) + ϕ], obtained one period T after time t, is greater than cos(ωt + ϕ) by 2π. Larry says that it is greater by the addition of 1.00 to cos(ωt + ϕ). Which one, if either, is correct?

Answer 1

No one is right

Step-by-step explanation:

John Case:

The function
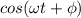`cos(\omega t +\phi)` is defined between -1 and 1, So it is not possible obtain a value
`2\pi` greater.

In addition, if you move the function cosine a T Value, and T is the Period, the function take the same value due to the cosine is a periodic function.

Larry case:

Is you have
`f=1+cos(\omega t +\phi)`, the domain of this is [0,2].

it is equivalent to adding 1 to the domain of the
`f=1+cos(\omega t +\phi)`, and its mean that the function
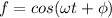`f=cos(\omega t +\phi)`, in general, is not greater than
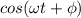`cos(\omega t +\phi)`.