Answer:
FC vector representation
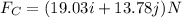
Magnitude of FC
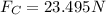
Vector direction FC
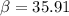 degrees: angle that forms FC with the horizontal
degrees: angle that forms FC with the horizontal
Step-by-step explanation:
Conceptual analysis
Because the particle C is close to two other electrically charged particles, it will experience two electrical forces and the solution of the problem is of a vector nature.
The directions of the individual forces exerted by qA and qB on qC are shown in the attached figure; The force (FAC) of qA over qC is repulsive because they have equal signs and the force (FBC) of qB over qC is attractive because they have opposite signs.
The FAC force is up in the positive direction and the FBC force forms an α angle with respect to the x axis.
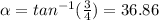 degrees
degrees
To calculate the magnitudes of the forces we apply Coulomb's law:
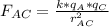 Equation (1): Magnitude of the electric force of the charge qA over the charge qC
Equation (1): Magnitude of the electric force of the charge qA over the charge qC
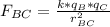 Equation (2) : Magnitude of the electric force of the charge qB over the charge qC
Equation (2) : Magnitude of the electric force of the charge qB over the charge qC
Known data
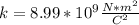
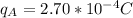
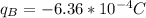
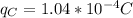
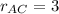
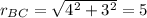
Problem development
In the equations (1) and (2) to calculate FAC Y FBC:
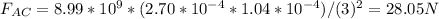
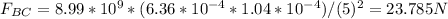
Components of the FBC force at x and y:
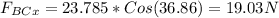
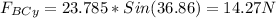
Components of the resulting force acting on qC:
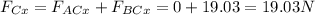
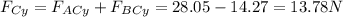
FC vector representation
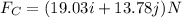
Magnitude of FC
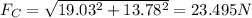
Vector direction FC
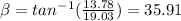 degrees: angle that forms FC with the horizontal
degrees: angle that forms FC with the horizontal