Question

Particle A of charge 2.70 10-4 C is at the origin, particle B of charge -6.36 10-4 C is at (4.00 m, 0), and particle C of charge 1.04 10-4 C is at (0, 3.00 m). We wish to find the net electric force on C.

Answer 1

FC vector representation

`F_(C) =(19.03i+13.78j)N`

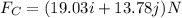
Magnitude of FC

`F_(C)=23.495N`

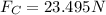
Vector direction FC

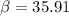`\beta=35.91` degrees: angle that forms FC with the horizontal

Step-by-step explanation:

Conceptual analysis

Because the particle C is close to two other electrically charged particles, it will experience two electrical forces and the solution of the problem is of a vector nature.

The directions of the individual forces exerted by qA and qB on qC are shown in the attached figure; The force (FAC) of qA over qC is repulsive because they have equal signs and the force (FBC) of qB over qC is attractive because they have opposite signs.

The FAC force is up in the positive direction and the FBC force forms an α angle with respect to the x axis.

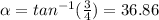`\alpha = tan^(-1)((3)/(4)) = 36.86` degrees

To calculate the magnitudes of the forces we apply Coulomb's law:

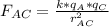`F_(AC) = (k*q_(A)*q_(C))/(r_(AC)^2)` Equation (1): Magnitude of the electric force of the charge qA over the charge qC

`F_(BC) = (k*q_(B)*q_(C))/(r_(BC)^2)` Equation (2) : Magnitude of the electric force of the charge qB over the charge qC

Known data

`k=8.99*10^9 (N*m^2)/(C^2)`

`q_(A)=2.70*10^(-4) C`

`q_(B)=-6.36*10^(-4) C`

`q_(C)=1.04*10^(-4) C`

`r_(AC) =3`

`r_(BC)=√(4^2+3^2) = 5`

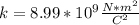
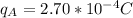
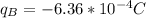
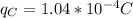
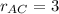
Problem development

In the equations (1) and (2) to calculate FAC Y FBC:

`F_(AC) =8.99*10^9*(2.70*10^(-4)* 1.04*10^(-4))/(3)^2=28.05N`

`F_(BC) =8.99*10^9*(6.36*10^(-4)* 1.04*10^(-4))/(5)^2=23.785N`

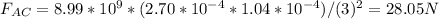
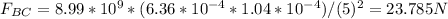
Components of the FBC force at x and y:

`F_(BCx)=23.785 *Cos(36.86)=19.03N`

`F_(BCy)=23.785 *Sin(36.86)=14.27N`

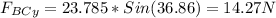
Components of the resulting force acting on qC:

`F_(Cx) = F_(ACx)+ F_(BCx)=0+19.03=19.03N`

`F_(Cy) = F_(ACy)+ F_(BCy)=28.05-14.27=13.78N`

FC vector representation

`F_(C) =(19.03i+13.78j)N`

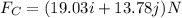
Magnitude of FC

`F_(C)= √(19.03^2+13.78^2) =23.495N`

Vector direction FC

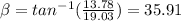`\beta = tan^(-1) ((13.78)/(19.03))=35.91` degrees: angle that forms FC with the horizontal