Question

Let u = -8i + 3j and v = 6i - j. Find (u + v)^2 - (u - v)^2.

Answer 1

Answer: The required value of the given expression is -204.

Step-by-step explanation: We are given the following two vectors :

`u=-8i+3j,\\\\v=6i-j.`

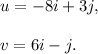
We are to find the value of the following :

`(u+v)^2-(u-v)^2.`

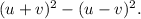
We will be using the following identities :

`i.j=j.i=0,\\\\i^2=j^2=1.`

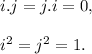
Therefore, the value of the given expression can be evaluated as follows :

`(u+v)^2-(u-v)^2\\\\=(u^2+2uv+v^2)-(u^2-2uv+v^2)\\\\=4uv\\\\=4(-8i+3j)(6i-j)\\\\=4(-48i^2+8ij+18ji-3j^2)\\\\=4(-48*1-3*1)\\\\=4(-48-3)\\\\=-204.`

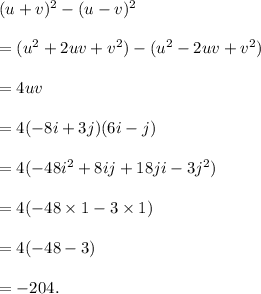
Thus, the required value of the given expression is -204.