Answer:
(C) 18(1 + √ 3)
Explanation:
Given,
In triangle ABC,
AC = 12 unit,
m∠A = 30°,
m∠B = 45°,
Let D∈AB such that CD ⊥ AB,
In triangle ADC,
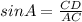
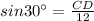
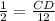
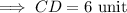 ,
,
By the pythagorean theorem,
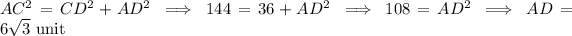
Now, in triangle CDB,
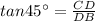
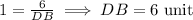
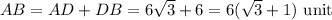
Hence, the area of the triangle ABC =
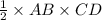
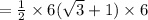
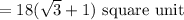
Option 'C' is correct.