Answer:
0.0256 m
Step-by-step explanation:
initial speed of electron, u = 3 x 10^6 m/s
Final speed of electron, v = 0 m/s
Electric field strength, E = 1 x 10^3 N/C
Charge on electron, q = 1.6 x 10^-19 C
mass of electron, m = 9.1 x 10^-31 kg
The electron experiences an electric force due to electric field which is given by
F = q E
Where, f be the electric force, and E be the strength of electric field.
Let a be the acceleration of electron
So,
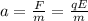
where, m is the mass of electron
By substituting the values, we get
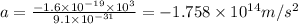
Let the distance traveled by the electron before coming to rest is s.
Use third equation of motion
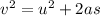
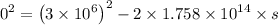
s = 0.0256 m