Question

Let f be strictly convex. If f has a minimum, show that it is unique. (Hint: assume there are two minima x1, x2 and derive a contradiction using the definition of convexity.)

Answer 1

Answer: Ok, i will use the hint provided.

We call x1 and x2 to te two mínima of f, that is
`(df)/(dx) (x1) = 0, (df)/(dx) (x2) = 0`.

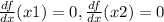The convexity condition says that, if f is differentiable, then the graph of f(x) lays above all the tangents between X and Y, if Y>X then

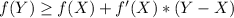`f(Y) \geq  f(X) + f'(X)*(Y-X)` where
`f'(x) = (df)/(dx) (x)`.

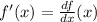then, if we took Y = x1 and X = x2, we have
`f(x1) \geq  f(x2)` because f'(x2) = 0.

now if we took Y = x2 and X = x1, we have
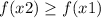`f(x2) \geq  f(x1)` because f'(x1) = 0.

Then, x1 = x2. Which implies that we only have one minima.