Question

Sumeet is building two types of birdhouses. The more traditional type takes 4 pieces of wood and 2 hours to build. The more lavish type takes 10 pieces of wood and 7 hours to build. If he has a total of 46 pieces of wood and 29 hours to work, then how many of each type of birdhouse can he build?

Answer 1

The no. of traditional type birdhouses are 4 and the no. of lavish type birdhouses are 3.

Explanation:

Let x be the no. of traditional type birdhouses

The more traditional type takes 4 pieces of wood and 2 hours to build.

One house requires wood = 4

x houses requires wood = 4x

One house requires time = 2 hours

x houses requires time = 2x

Let y be the no. of lavish type birdhouses

The more lavish type takes 10 pieces of wood and 7 hours to build.

One house requires wood = 10

y houses requires wood = 10y

One house requires time = 7 hours

y houses requires time = 7y

Now we are given that he has a total of 46 pieces of wood and 29 hours to work,

So, equations becomes :
`4x+10y = 46\\2x+7y=29`

Plot these equations on graph

`4x+10y = 46` ---Blue line

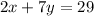`2x+7y=29` ---Green line

Refer the attached figure

The intersection point provides the solution

Intersection point : (4,3)

So, x = 4 and y = 3

Hence the no. of traditional type birdhouses are 4 and the no. of lavish type birdhouses are 3.