Answer:
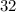 m/s
m/s
Step-by-step explanation:
 = angle of launch of the ball = 25 deg
= angle of launch of the ball = 25 deg
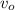 = speed of launch of the golf ball = ?
= speed of launch of the golf ball = ?
Consider the motion along vertical direction
 = initial velocity along y-direction =
= initial velocity along y-direction =
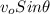 =
=

 = time of travel in air = ?
= time of travel in air = ?
 = vertical displacement = 0 m
= vertical displacement = 0 m
 = acceleration due to gravity = 9.8 m/s²
= acceleration due to gravity = 9.8 m/s²
Using the equation
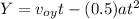

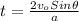 eq-1
eq-1
Consider the motion along horizontal direction
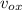 = initial velocity along x-direction =
= initial velocity along x-direction =
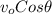 =
=
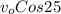
 = time of travel in air = ?
= time of travel in air = ?
 = horizontal displacement = 80.0438 m
= horizontal displacement = 80.0438 m
Using the equation
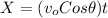
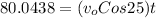
using eq-1

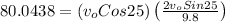
 m/s
m/s