Question

Strontium 90 is a radioactive waste product from nuclear reactors. It has a half-life of 29 years. How many years will it take for a quantity of strontium-90 to decay to 1/16 of its original mass?

Answer 1

It will take 116 years for a quantity of strontium-90 to decay to 1/16 of its original mass, as four half-lives are required to reach this fraction.

Step-by-step explanation:

To calculate the time it will take for a quantity of strontium-90 to decay to 1/16 of its original mass, we can use the concept of half-lives. One half-life (29 years) results in a decay to 1/2 of the original quantity. Here are the steps:

First half-life: The quantity becomes 1/2 of the original.

Second half-life: The quantity becomes 1/2 of 1/2, which is 1/4 of the original.

Third half-life: The quantity becomes 1/2 of 1/4, which is 1/8 of the original.

Fourth half-life: The quantity becomes 1/2 of 1/8, which is 1/16 of the original.

To get to 1/16, we need four half-lives. Therefore, the time it will take is 4 half-lives × 29 years/half-life = 116 years.

Answer 2

116 years

Step-by-step explanation:

For this type of problems we have to use the formula that model the radioactive decay, that it's:

`N = N_(0) e^(-\lambda t)`,

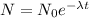where
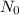`N_(0)` correspond to the initial amount of mass of the element,
`\lambda` correspond to the decay constant of the element,
`t` correspond the time measured in years and
`N` correspond to the amount of mass left after
`t` years.

In this case the original amount of mass is unknown but we don't need it to resolve the question, so let's make use of the half-life data that we've been given:

If the original amount of mass is
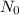`N_(0)` then after
`t` = 29 years the amount of mass left is the half of
`N_(0)`.

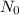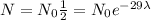`N = N_(0)(1)/(2) =  N_(0)e^(-29\lambda )`, we cancel equal terms on both sides and obtain that
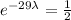`e^(-29\lambda) = (1)/(2)`, now we take natural logarithm on both sides (due to exponential function and logarithmic function are inverses) and then we obtain
`\lambda` by dividing for -29, so
`\lambda = (-log((1)/(2)))/(29)`

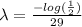
Now we know the formula that model the radioactive decay for Strontium-90:

`N = N_(0)e^{(log((1)/(2)))/(29)t}`

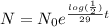
So we've been asked for the time in years were the mass left will be the 1/16 of it's original mass,

By that time
`t` in years we have that
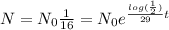`N = N_(0)(1)/(16)  = N_(0)e^{(log((1)/(2)))/(29)t}`, we cancel equal terms and take natural logorithm on both sides
`log((1)/(16))  = (log((1)/(2)))/(29)t}`, finally we obtain after dividing that
`t = (29 log((1)/(16)))/(log((1)/(2))) = 116` years