Question

Two window washers start at the heights shown. (A: 21 ft high rising 8 in per second. The other is 50 feet high descending 11inches per second) one is rising one is descending. How long does it take for the two window washers to reach the same height? Explain

Answer 1

For this case, the first thing we are going to do is write the generic equation of motion for the vertical axis.

We have then:

`h = \frac {1} {2} gt ^ 2 + vo * t + h0`

Where,

• g: acceleration of gravity
• vo: initial speed
• h0: initial height

For the first body:

`h1 = \frac {1} {2} gt ^ 2 + \frac {8} {12} * t + 21`

For the second body:

`h2 = \frac {1} {2} gt ^ 2 - \frac {11} {12} * t + 50`

By the time both bodies have the same height we have:

`h1 = h2\\`

`\frac {1} {2} gt ^ 2 + \frac {8} {12} * t + 21 = \frac {1} {2} gt ^ 2 - \frac {11} {12} * t + 50`

Rewriting we have:

`\frac {8} {12} * t + 21 = - \frac {11} {12} * t + 50`

`\frac {8} {12} * t + \frac {11} {12} * t = 50 - 21`

`\frac {19} {12} * t = 29`

Clearing time:

`t = 29 (\frac {12} {19})\\t = 18.31s`

Answer:

it takes 18.31s for the two window washers to reach the same height

Answer 2

After 18.32 seconds two window washers will reach the same height.

Explanation:

Let h is the height at which a window washer A meats other window washer B.

A is ascending with the speed = 8 inch per second

At present A is at the height = 21 ft or 21×12 inches = 252 inches

If they meet after time t then the equation representing this relation between height and time will be

h = 252 + 8t ---------(1)

Other window washer B is at height = 50 feet or 50×12 = 600 inch

B is coming down with the speed = 11 inches per second

After time t their height will be h = 600 - 11t --------(2)

Now equating both the equations

252 + 8t = 600 - 11t

8t + 11t + 252 = 600

19t = 600 - 252

19t = 348

t =
`(348)/(19)`

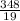
t = 18.32 seconds