Question

Suppose the population of a certain city is 5358 thousand. It is expected to decrease to 4565 thousand in 50 years. Find the percent decrease. The percent decrease is approximately nothing​%. ​(Round to the nearest​ tenth.)

Answer 1

The population decreases at the rate of 0.32% a year.

Explanation:

The population of this certain city can be modeled by this following differential equation.

`(dP)/(dt) = Pr`

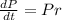
where r is the growth rate(r>0 means that the population increases, r < 0 it decreases).

We can solve this by the variable separation method. We have that:

`(dP)/(P) = rdt`

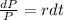
Integrating both sides, we have

`ln{P} = rt + P(0)`

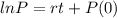
where P(0) is the initial population.

To find P in function of t, we apply the exponential to both sides.

`e^{ln{P}} = e^(rt + P(0))`

`P(t) = P(0)e^(rt)`

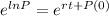
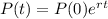
The initial population of the city 5,358,000. So P(0) = 5,358,000.

It decreases to 4,565,000 in 50 years. So P(50) = 4,565,000.

Applying to the bold equation:

`5,358,000 = 4,565,000e^(50r)`

`e^(50r) = 1.174`

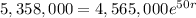
To find the growth rate, we apply ln to both sides.

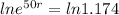
`ln{e^(50r)} = ln{1.174}`

`50r = 0.16`

r =
`(0.16)/(50) = 0.0032 = 0.32%`

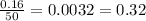
The population decreases at the rate of 0.32% a year.