Answer:
The population decreases at the rate of 0.32% a year.
Explanation:
The population of this certain city can be modeled by this following differential equation.
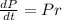
where r is the growth rate(r>0 means that the population increases, r < 0 it decreases).
We can solve this by the variable separation method. We have that:
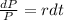
Integrating both sides, we have
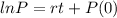
where P(0) is the initial population.
To find P in function of t, we apply the exponential to both sides.
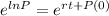
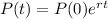
The initial population of the city 5,358,000. So P(0) = 5,358,000.
It decreases to 4,565,000 in 50 years. So P(50) = 4,565,000.
Applying to the bold equation:
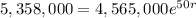
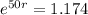
To find the growth rate, we apply ln to both sides.
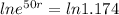

r =
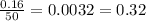
The population decreases at the rate of 0.32% a year.