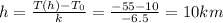Answer:
10 km
Step-by-step explanation:
We are told that the temperature at the surface is
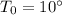
and that the rate of drop of the temperature vs height is
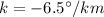
Therefore we can write the temperature at a generic altitude h as
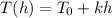
If we call h the height of the tropopause, we have
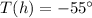
Therefore we can solve the equation to find h, the height of the tropopause: