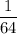Answer: (D)
Explanation:
Given : An insurance company determines that N, the number of claims received in a week, is a random variable with
![P[N=n]=((1)/(2))^(n+1)](https://img.qammunity.org/2020/formulas/mathematics/college/7fahj6oe8edehuza3sicu4l1i7ojaf5ui3.png) , where n > 0 .
, where n > 0 .
To determine the probability that exactly seven claims will be received during a given two week period.
Let n is the number of claims during first week (
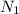 ) the 7-n is the number of claims during second week (
) the 7-n is the number of claims during second week (
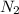 ).
).
Then , we have
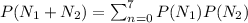
[ ∵ The number of claims received in a given week is independent of the number of claims received in any other week. ]
=
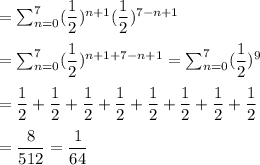
Hence, the probability that exactly seven claims will be received during a given two week period =