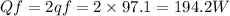Question

Two long copper rods of diameter D 10 mm are soldered together end to end, with solder having a melting point of 650 C. The rods are in air at 25 C with a convection coefficient of 10 W/m2 K. What is the minimum power input needed to effect the soldering?

Answer 1

125pi W/m

Step-by-step explanation:

This is the formula for heat transfer by convection

Q=hA(T2-T1)

Q=Power

h=convection coefficient

A=area

T2= temperature of melting point

T1=temperature of air

Area of tow rods

A=2*pi*D=2*pi*0.01=pi/50

Q=10*(´pi/50)(650-25)

Q=125pi W/m

Answer 2

Qf 194.2 W

Step-by-step explanation:

Given data:

Diameter of copper rod D is 0.01 ,

Temperature at junction is Tb = 650 + 273 = 923 K

Temperature of air is 15+273 = 288 K

`Tmean = (923 + 288)/(2) = 605.5 K`

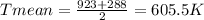
For temperature 605.5 degree celcius thermal conductivity is K = 379 W/m K

Heat transfer is calculated as

`qf = √(hPkAc(Tb -T\infty))`

`qf = \sqrt{h\pi D k(\pi)/(4) D^2 (Tb -T\infty)}`

`qf = \sqrt{25 \pi * 0.01* 379 * (\pi)/(4) * 0.01^2(920 -288)}`

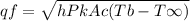
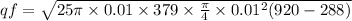
qf = 97.1 W

Hence, the rate of heat is

`Qf = 2qf = 2* 97.1 = 194.2 W`