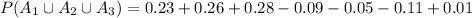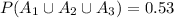Answer:
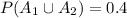
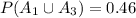
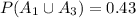
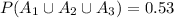
Explanation:
For the probability of events not mutually exclusive we have to add the probability of each event and substract the probability of the intersection of the events:
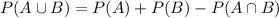
For the given information we can deduce the following probabilities:
<probability of the union of A_1 and A_2>
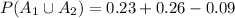
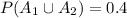
<probability of the union of A_1 and A_3>
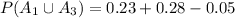
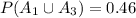
<probability of the union of A_2 and A_3>
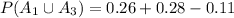
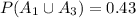
We can also use the given information to get the probability of the union of
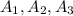 . For that purpose we use the next formula:
. For that purpose we use the next formula:
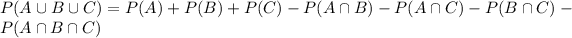
So we the given information: