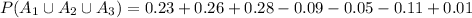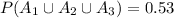Question

A computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = 0.23, P(A2) = 0.26, P(A3) = 0.28, P(A1 ∩ A2) = 0.09, P(A1 ∩ A3) = 0.05, P(A2 ∩ A3) = 0.11, P(A1 ∩ A2 ∩ A3) = 0.01. Use the probabilities given above to compute the following probabilities, and explain in words the meaning of each one. (Round your answers to four decimal places.)

Answer 1

`P(A_1 \cup A_2) = 0.4`

`P(A_1 \cup A_3) = 0.46`

`P(A_1 \cup A_3) = 0.43`

`P(A_1 \cup A_2 \cup A_3) = 0.53`

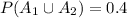
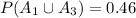
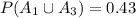
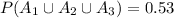
Explanation:

For the probability of events not mutually exclusive we have to add the probability of each event and substract the probability of the intersection of the events:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

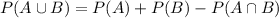
For the given information we can deduce the following probabilities:

<probability of the union of A_1 and A_2>

`P(A_1 \cup A_2) = 0.23 + 0.26 - 0.09`

`P(A_1 \cup A_2) = 0.4`

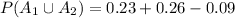
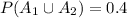
<probability of the union of A_1 and A_3>

`P(A_1 \cup A_3) = 0.23 + 0.28 - 0.05`

`P(A_1 \cup A_3) = 0.46`

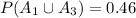
<probability of the union of A_2 and A_3>

`P(A_1 \cup A_3) = 0.26 + 0.28 - 0.11`

`P(A_1 \cup A_3) = 0.43`

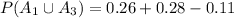
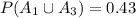
We can also use the given information to get the probability of the union of
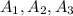`A_(1), A_(2),  A_(3)` . For that purpose we use the next formula:

`P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) - P(A \cap B \cap C)`

So we the given information:

`P(A_1 \cup A_2 \cup A_3) = 0.23 + 0.26 + 0.28 - 0.09 - 0.05 - 0.11 + 0.01`

`P(A_1 \cup A_2 \cup A_3) = 0.53`