Question

The engine of a locomotive exerts a constant force of 8.1*10^5 N to accelerate a train to 68 km/h. Determine the time (in min) taken for the train of mass 1.9*10^7 kg to reach this speed from rest.

Answer 1

Step-by-step explanation:

It is given that,

Force acting on the engine,
`F=8.1* 10^5\ N`

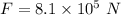
Initial speed of the engine, u = 0 (at rest)

Final speed of the engine, v = 68 km/h = 18.88 m/s

Mass of the train,
`m=1.9* 10^7\ kg`

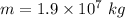
We need to find the time taken by the train. Firstly, we will find the acceleration of the engine from Newton's second law of motion as :

`a=(F)/(m)`

`a=(8.1* 10^5)/(1.9* 10^7)`

`a=0.042\ m/s^2`

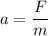
Now using first equation of motion to find time taken as :

`v=u+at`

`t=(v-u)/(a)`

`t=(18.88-0)/(0.042)`

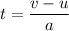
t = 449.52 seconds

or

t = 7.49 minutes

So, the time taken for the train to reach this speed is 7.49 minutes. Hence, this is the required solution.

Answer 2

Answer:443.1 s

Step-by-step explanation:

Given

Engine of a locomotive exerts a force of
`8.1* 10^5 N`

Mass of train
`=1.9* 10^7`

Final speed (v)
`=68 km/h \approx 18.88 m/s`

F=ma

so
`acceleration(a) =(F)/(m)=(8.1* 10^5)/(1.9* 10^7)`

`a=0.042631 m/s^2`

and acceleration is

`a=(v-u)/(t)`

`0.042631=(18.88-0)/(t)`

`t=443.089 \approx 443.1 s`