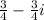Answer:
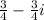
Explanation:
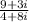
I assume you want to rationalize the denominator (make it real). To do this, we will multiply top and bottom by bottom's cojugate.
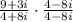
Use foil on top.
On bottom, since you are multiplying conjugates all you have to do is first times first and last times last.
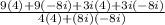
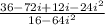
Recall
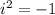 .
.
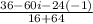
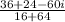
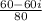
Both the numerator and denominator share a common factor of 20:
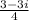
You could also seperate the fraction like so: