Question

9+3i divided by 4+8i

Answer 1

`(3)/(4)-(3)/(4)i`

Explanation:

`(9+3i)/(4+8i)`

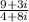
I assume you want to rationalize the denominator (make it real). To do this, we will multiply top and bottom by bottom's cojugate.

`(9+3i)/(4+8i) \cdot (4-8i)/(4-8i)`

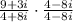
Use foil on top.

On bottom, since you are multiplying conjugates all you have to do is first times first and last times last.

`(9(4)+9(-8i)+3i(4)+3i(-8i))/(4(4)+(8i)(-8i))`

`(36-72i+12i-24i^2)/(16-64i^2)`

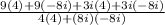
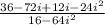
Recall
`i^2=-1`.

`(36-60i-24(-1))/(16+64)`

`(36+24-60i)/(16+64)`

`(60-60i)/(80)`

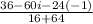
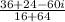
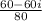
Both the numerator and denominator share a common factor of 20:

`(3-3i)/(4)`

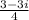
You could also seperate the fraction like so:

`(3)/(4)-(3)/(4)i`