Question

A glass plate whose index of refraction is 1.57 is immersed in a liquid. The surface of the glass is inclined at an angle of 54° with the vertical. A horizontal ray in the glass is incident on the interface. The liquid is an oil whose index of refraction is 1.40. The incident horizontal ray refracts at the interface. What is the angle that the refracted ray, in the oil, makes with the horizontal?

Answer 1

The angle that the refracted ray in the oil makes with the horizontal is 65.0°.

Step-by-step explanation:

Given that,

Index of refraction of glass = 1.57

Angle = 54°

Index of refraction of oil = 1.40

We need to calculate the angle that the refracted ray, in the oil, makes with the horizontal

Using Snell's law

`n_(i)\sin i=n_(r)\sin r`

Put the value into the formula

`1.57*\sin54=1.40\sin r`

`\sin r=(1.57*\sin54)/(1.40)`

`\sin r=0.907`

`r=65.0^(\circ)`

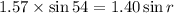
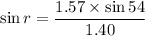
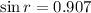
Hence, The angle that the refracted ray in the oil makes with the horizontal is 65.0°.