Question

The ratio of three consecutive angles in a cyclic quadrilateral is $2:3:4$. Find the largest angle of the quadrilateral, in degrees.

Answer 1

The largest angle of the quadrilateral is 120°.

Explanation:

Given : The ratio of three consecutive angles in a cyclic quadrilateral is 2:3:4

To find : The largest angle of the quadrilateral, in degrees ?

Solution :

Let the ration be 'x',

So, The consecutive angles are 2x , 3x and 4x.

We know that, Opposite angles of cyclic quadrilateral is 180°.

i.e.
`2x+4x=180`

`6x=180`

`x=(180)/(6)`

`x=30`

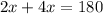
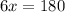
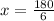
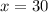
The angles became,

`2x=2(30)=60`

`3x=3(30)=90`

`4x=4(30)=120`

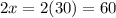
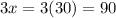
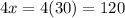
We know that sum of all angles of quadrilateral is 360°,

Let the fourth angle be A,

`A+60+90+120=360`

`A+270=360`

`A=360-270`

`A=90`

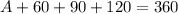
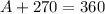
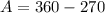
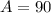
Therefore, Among all the angles the largest angle of the quadrilateral is 120°.