Answer:
number of cycles = 4.68 × 10⁴ cycles
Step-by-step explanation:
In damped RLC oscillation
voltage (V(t)) = V_o\ e^{-\dfrac{tR}{2L}}............(1)
given,
C = 0.17μF = 0.17 × 10⁻⁶ F
R = 1.4 Ω
L = 15 m H = 15 × 10⁻³ H V(t) = V₀/2
From the equation (1)
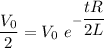
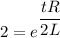
taking log both side
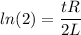
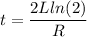
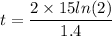
t = 14.85 sec
time period


T = 3.172 × 10⁻⁴
number of cycle =
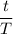
=
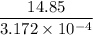
number of cycles = 4.68 × 10⁴ cycles