Question

A damped LC circuit consists of a 0.17 μF capacitor and a 15 mH inductor with resistance 1.4Ω. How many cycles will the circuit oscillate before the peak voltage on the capacitor drops to half its initial value? Express your answer using two significant figures.

Answer 1

number of cycles = 4.68 × 10⁴ cycles

Step-by-step explanation:

In damped RLC oscillation

voltage (V(t)) = V_o\ e^{-\dfrac{tR}{2L}}............(1)

given,

C = 0.17μF = 0.17 × 10⁻⁶ F

R = 1.4 Ω

L = 15 m H = 15 × 10⁻³ H V(t) = V₀/2

From the equation (1)

`(V_0)/(2) = V_0\ e^{-(tR)/(2L)}`

`2 = e^{(tR)/(2L)}`

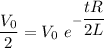
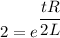
taking log both side

`ln ( 2 ) = (tR)/(2L)`

`t = (2 L ln(2))/(R)`

`t = (2 * 15 ln(2))/(1.4)`

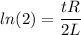
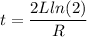
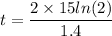
t = 14.85 sec

time period

`T= 2\pi √(LC)`

`T= 2\pi \sqrt{0.015 * 0.17 * 10^(-6)}`

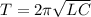
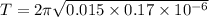
T = 3.172 × 10⁻⁴

number of cycle =
`(t)/(T)`

=
`(14.85)/(3.172 * 10^(-4))`

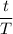
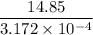
number of cycles = 4.68 × 10⁴ cycles