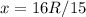Answer:
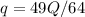
and
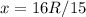
Step-by-step explanation:
See attached figure.
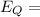 E due to sphere
E due to sphere
 E due to particule
E due to particule
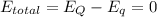 (1)
(1)
according to the law of gauss and superposition Law:
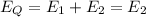 ; electric field due to the small sphere with r1=R/4
; electric field due to the small sphere with r1=R/4
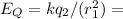
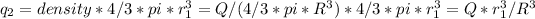
then:
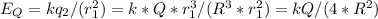 (2)
(2)
on the other hand, for the particule:
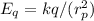
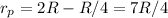 ⇒
⇒
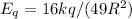 (3)
(3)
We replace (2) y (3) in (1):

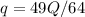
--------------------
if R<x<2R AND
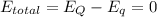
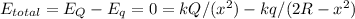
remember that
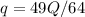
then:
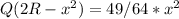
solving:
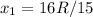
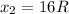
but: R<x<2R
so :