Question

A moving particle fragments or decays into a particle moving at .53c, mass 135 MeV/c2, and a particle moving at .98c, mass 938 MeV/c2 - both going in the same direction. Calculate the mass and speed of the initial particle.

Answer 1

M = 1073 Mev/c2

u = 0.95 C

Step-by-step explanation:

given data:

m1 =135 Mev/c2

v1 = 0.53 c

m2 = 938 Mev/c2

v2 = 0.98 c

from conservation of momentum principle we have

`\frac{mu}{\sqrt{1-(u^2)/(C^2)}} = \frac{m1v1}{\sqrt{1-(V1^2)/(C^2)}} +\frac{m1v1}{\sqrt{1-(V2^2)/(C^2)}}`

`\frac{mu}{\sqrt{1-(u^2)/(C^2)}} = (135*0.53c)/(0.848) +(938*0.98c)/(0.2)`

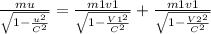
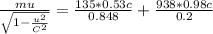
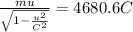`\frac{mu}{\sqrt{1-(u^2)/(C^2)}} = 4680.6 C` ...............1

Total mass of INITIAL particle M =m1+m2 = 1073 Mev/c2

using equation 1

`\frac{1073 u}{\sqrt{1-(u^2)/(C^2)}}= 4680.6C`

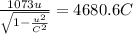
solving for u we get

u = 0.95 C