Answer:
M = 1073 Mev/c2
u = 0.95 C
Step-by-step explanation:
given data:
m1 =135 Mev/c2
v1 = 0.53 c
m2 = 938 Mev/c2
v2 = 0.98 c
from conservation of momentum principle we have
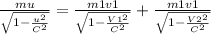
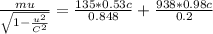
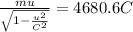 ...............1
...............1
Total mass of INITIAL particle M =m1+m2 = 1073 Mev/c2
using equation 1
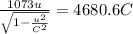
solving for u we get
u = 0.95 C