Question

Find the exponential function P(t)=P0a^t where P(2)=5 and P(4)=10

Answer 1

`P(t)=(5)/(2) \cdot (√(2))^t`

Explanation:

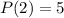`P(2)=5` meants when
`t=2`, that the value for
`P(t)` is 5.

So this gives us this equation:

`5=P_0 \cdot a^2`

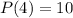`P(4)=10` meants when
`t=4`, that the value for
`P(t)` is 10.

So this gives us this equation:

`10=P_0 \cdot a^4`

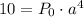
So I take equation 2 and divide it be equation 1 I get:

`(10)/(5)=(P_0 \cdot a_4)/(P_0 \cdot a_2)`

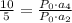
Simplifying:

`2=a^2`

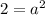
Since the base for an exponential function can't be negative then
`a=√(2)`.

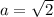So plugging into one of my equations I began with gives me an equation to solve for the initial value,
`P_0`:

`5=P_0 \cdot (√(2))^2`

`5=P_0 \cdot 2`

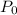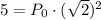
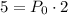
Divide both sides by 2:

`(5)/(2)=P_0`

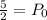
The function is:

`P(t)=(5)/(2) \cdot (√(2))^t`