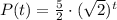Answer:
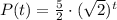
Explanation:
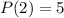 meants when
meants when
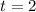 , that the value for
, that the value for
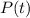 is 5.
is 5.
So this gives us this equation:
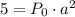
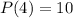 meants when
meants when
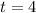 , that the value for
, that the value for
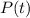 is 10.
is 10.
So this gives us this equation:
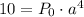
So I take equation 2 and divide it be equation 1 I get:
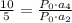
Simplifying:
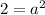
Since the base for an exponential function can't be negative then
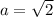 .
.
So plugging into one of my equations I began with gives me an equation to solve for the initial value,
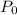 :
:
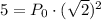
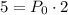
Divide both sides by 2:
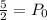
The function is: