Answer:
[-1,6)U(6, ∞)
Explanation:

In functions that have a square root, the radicand (the inside of the root) has to be ≥0. Otherwise, you would be dealing with imaginary numbers.
So, in our function,

We have two factors in our denominator. Note that you cannot divide by 0. So to find where x cannot be, we have to set the denominator to 0.
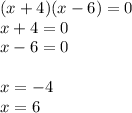
X cannot be either -4 or 6.
So, x has to be greater than or equal to -1 and cannot equal -4 or 6.
x≥-1, x≠6